Dibujo Técnico: Sistemas de Representación.

SISTEMAS DE REPRESENTACIÓN

Ámbos, Sistema Diédrico y Sistema Triédrico, son SISTEMAS DE REPRESENTACIÓN.

Los Sistemas de Representación son la base para reflejar las tres dimensiones que tiene un objeto en el espacio. En el caso del Dibujo Técnico sobre un soporte que solo tiene dos dimensiones, es decir nuestro papel.

Para hacer esto y representar las vistas posibles de un objeto se trazarán sus proyecciones sobre unos planos imaginarios llamados Planos de Proyección.

En estos Planos de Proyección se representarán las vistas Planta, Alzado y Perfil. Pues bien esto es lo que son los Sistemas de Representación.

Existen otros Sistemas de Representación más o menos prácticos pero son dos los Sistemas que han sido adoptados como universales dentro del mundo del Dibujo Técnico. Son el Sistema Diédrico y Sistema Triédrico.

Tanto el Sitema Diédrico Ortogonal o también denominado de Monge ( por el personaje quién lo descubrió ) como el Sistema Triédrico, son un métodos analíticos que permiten deducir la forma de un volumen u objeto y su situación en el espacio, aunque si tenemos que comentar ambos son poco directos. Para solucionar este inconveniente y como he dicho anteriormente, existen otros Sistemas que ofrecen una visión mas completa, inmediata y aproximada de la realidad del volumen u objeto representado.

Este Sistema son las llamadas Perspectivas.

El Sistema de Representación de las Perspectivas, el mundo de las Perspectivas que es muy amplio, nos permite dibujar en volumen la forma que se desea representar. Existen varios tipos de Perspectivas y dependiendo del tipo de Perspectiva que se adopte en cada caso se podrá llegar a obtener una imagen del objeto que prácticamente coincidirá con la que se tendría al observar el objeto en verdadera magnitud en la realidad, de forma directa.

Vamos a ver cada una de estas formas de representación de una forma más analítica, profunda y práctica para llegar a comprenderlas verdaderamente.

A) SISTEMA DIÉDRICO

1 – División del Espacio en Cuadrantes o Diedros.

El Sistema Diédrico va a representar la forma de un objeto sobre dos planos ( di=dos / edro=plano ) que forman un ángulo recto entre sí.

Los Planos sobre los que se proyecta el objeto se denominan Plano Vertical ( PV ) y Plano Horizontal ( PH ).

La Línea de Tierra o Charnela ( LT ) es la recta que conforma la intersección de ambos Planos. La forma de representarlo en Planos es por las iniciales LT o también por dos trazos horizontales, uno a cada lado de la línea.

El Cuadrante o Diedro sobre el que se trabajará inicial normalmente es el Primero.

Y otra de las cosas que tenemos que tener muy en cuenta, sobre todo al principio o aprendizaje del Sistema Diédrico, es que se denominará Plano Bisectoral al Plano que forma 45º con los Planos PV y PH que pasa evidentemente por la LT.

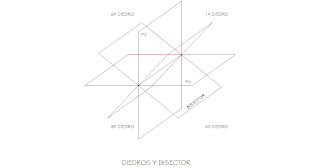
Observamos que al dibujar en Planos u Hojas de papel distintos, cada una de las Proyecciones ( manteniendo entre ambas la relación de sus distintas partes ) se complicaría gravemente su trazado.

Para evitar esto se ha llegado a una simplificación que resuelve dicho problema.

Si el PH girara a 90º alrededor de la LT , éste formaría con el PV un solo Plano. De esta manera podrán desarrollarse las dos Proyecciones en una sola hoja de papel o Plano.

Vamos a observar ahora en este dibujo la representación de un volumen realizado con el Sistema Diédrico.

2 – Proyecciones.

Si en dos Planos ilimitados que se cortan formando entre sí un ángulo recto se toma un punto, como ejemplo, se verá que al situarlo en P, es decir, en el espacio entre ambos Planos su proyección sobre uno y otro determinará su planta y su alzado.

Para diferenciar las Proyecciones y el Punto en el espacio, la anotación de éstas se realizará mediante letras minúsculas, colocando siempre un acento o comilla ( p´ ) únicamente sobre la letra que corresponde a su Proyección sobre el Plano Vertical.

Esto es todo lo que vamos a comentar del Sistema Diédrico. Es lo que define al Sistema Diédrico como un Sistema muy importante y base para comprender el siguiente Sistema, el cual va a representar un poco mejor la forma del objeto a representar en tres Dimensiones, con absoluta claridad para su comprensión.

B) SISTEMA TRIÉDRICO

En ocasiones, ya lo hemos mencionado anteriormente, las dos vistas que proporciona el Sistema Diédrico no son suficientes para describir en su totalidad el objeto a representar.

En este caso se recurrirá a otro Plano a mayores, sobre el que se proyectará el Perfil del objeto de la misma manera que se ha hecho antes con su alzado.

A este Sistema, con el que se obtendrán tres Vistas a partir de los tres Planos de Proyección, se le denomina Sistema Triédrico.

Tenemos que aclarar que no se trata de un nuevo Sistema de Proyección, sino de una nueva variante ampliada del Sistema Diédrico cuya finalidad consiste en tener una mayor información del Objeto a representar.

A este tercer Plano sobre el que se Proyecta el Perfil del Objeto se le denomina Plano de Perfil ( PP )

En este caso, la anotación del Punto P va a ser una letra minúscula seguida de dos comas o comillas ( p´´ ).

La Proyección obtenida en el PP se abatirá sobre el mismo Plano en el que se encuentran las dos Proyecciones anteriores.

El Sistema Triédrico representa la forma del objeto sobre tres Planos: Vertical, Horizontal y de Perfil. Es una variante del Diédrico con la que se obtiene una mayor información del objeto a representar.

Vamos a ver las distintas Proyecciones que se pueden hacer de un objeto dentro del Sistema Triédrico.

Son Cuatro: 1- Proyección del Punto.

2- Proyección de la Recta.

3- Proyección del Plano.

4- Proyección de Volúmenes ( iniciación a la representación de Perspectivas ).

Vamos a verlos detenidamente de forma teórica y Práctica ( Gráfica ):

1 – Proyección del Punto.

La Proyección de un Punto sobre uno de los Planos de Proyección es la intersección de la perpendicular al Plano, trazada desde ese Punto.

Si hacemos una prueba podemos ver: abatimos el PH haciendo que las Proyecciones V y H formen un solo Plano. Entonces observamos que las representaciones del Punto sobre estos dos Planos están sobre una misma Línea, perpendicular a la Línea de tierra.

Como consecuencia, según la posición que ocupe el Punto en el espacio respecto a los Planos de Proyección su Representación Gráfica variará.

Para especificar las distintas posiciones del Punto vamos a referirnos a sus Proyecciones sobre los PV y PH. Según estas, un Punto en el espacio puede ocupar las siguientes posiciones:

a) Situado en el espacio PV y PH.

b) Situado en el Plano Vertical PV.

c) Situado en el Plano Horizontal PH.

d) Situado en los dos Planos, es decir, situado sobre la Línea de Tierra LT.

Las distancias del Punto a los Planos de Proyección se denominan de las siguientes maneras:

- Cota o Altura: la distancia que lo separa del Plano Horizontal PH.

- Alejamiento: la que lo separa del Plano Vertical PV.

- Distancia: la que la separa del Plano de Perfil PP ( en el caso de que se recurra al Sistema Triédrico para la Representación ).

La Cota será positiva si el punto está por encima del Plano Horizontal, en los Diedros 1.0 y 2.0.

Si está en el Plano Horizontal PH, la cota será cero.

Si está en el tercero y cuarto Diedro, la Cota será negativa.

El Alejamiento será positivo si está contenido en el primero y cuarto Diedro.

Si el punto está en el Plano Vertical PV, el Alejamiento será cero.

Si está en el segundo y tercer Diedro, el Alejamiento será negativo.

La Proyección de un Punto sobre uno de los Planos de Proyección se consigue trazando una perpendicular desde ese Punto hasta alcanzar su intersección con el Plano.

2 – Proyección de la Recta.

Como ya sabemos una Recta queda determinada por dos Puntos. Para hallar las Proyecciones de una Recta se determinan las Proyecciones de sus dos Puntos sobre cada uno de los Planos de Proyección, uniéndolos entre sí. La Proyección de la Recta sobre los Planos de Proyección PV y PH será siempre una línea recta, excepto cuando sea perpendicular a uno de ellos ( en ese caso, su representación sería un Punto ).

Se llaman Trazas de una Recta a las intersecciones que ésta puede provocar sobre cada uno de los Planos.

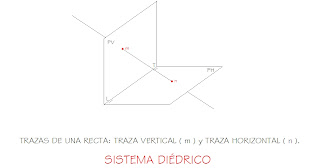
Son muchas las posiciones que puede adoptar la Recta respecto a los Planos de Proyección; las más importantes son las siguientes:

A ) Oblicua a los dos Planos de Proyección PV y PH.

B ) Oblicua al PH y paralela al PV.

C ) Oblicua al PV y paralela al PH.

D ) Paralela a los dos Planos.

E ) Perpendicular al Plano Vertical PV.

F ) Perpendicular al Plano Horizontal PH.

G ) Perpendicular a la Línea de Tierra LT, cortándola.

H ) Perpendicular a la Línea de Tierra LT, sin cortarla.

I ) Contenida en el Plano Vertical PV.

J ) Contenida en el Plano Horizontal PH.

3 – Proyección del Plano.

En este apartado se deben de tener en cuenta que las Proyecciones no son simplemente de Punto o Recta sobre Plano ( PH o PV ), sino de Plano sobre Plano. Recuérdese, en primer lugar, que la intersección entre dos Planos es una Línea Recta. Según esto, las Proyecciones de cada uno de los Planos se representarán por las Líneas de intersección con sus Planos de Proyección.

Según el Plano de Proyección sobre el que se realice la intersección se llamarán a dichas Líneas Trazas Verticales u Horizontales.

El Plano en el Espacio, al igual que la Recta y el Punto adoptará, respecto a los Planos de Proyección PV y PH, distintas posiciones; como en lo casos anteriores, sólo se enumerarán las más importantes:

A ) Oblicua a los dos Planos de Proyección PV y PH.

B ) Oblicuo al PH y perpendicular al PV.

C ) Oblicuo al PV y perpendicular al PH.

D ) Perpendicular a ambos Planos PV y PH o de perfil.

E ) Perpendicular al PH y paralelo al PV.

F ) Perpendicular al PV y paralelo al PH.

G ) Paralelo a la LT, cortado al PV y PH.

H ) Conteniendo a la LT.

Y por último,

4 – Proyección de Volúmenes.

Para hallar la Proyección de Volúmenes, se ha de aplicar lo explicado anteriormente sobre las Proyecciones de Punto, Recta y Plano; hay que tener en cuenta que un cuerpo se puede descomponer en un conjunto de Planos, que a su vez están formados por Rectas y Puntos.

Dentro de los Sistemas de Representación comentábamos al principio que son dos los Sistemas más empleados en dibujo técnico, siendo la base para otro tipo de Sistemas de Representación más completos que éstos. Estos Sistemas de Representación son el Sistema Diédrico y el Sistema Triédrico.

Tanto el Sitema Diédrico Ortogonal o también denominado de Monge ( por el personaje quién lo descubrió ) como el Sistema Triédrico, son un métodos analíticos que permiten deducir la forma de un volumen u objeto y su situación en el espacio, aunque si tenemos que comentar ambos son poco directos. Para solucionar este inconveniente y como he dicho anteriormente existen otros Sistemas que ofrecen una visión mas completa, inmediata y aproximada de la realidad del volumen u objeto representado. Este Sistema son las llamadas Perspectivas. El Sistema de Representación de las Perspectivas, el mundo de las Perspectivas que es muy amplio, nos permite dibujar en volumen la forma que se desea representar. Existen varios tipos de Perspectivas y dependiendo del tipo de Perspectiva que se adopte en cada caso se podrá llegar a obtener una imagen del objeto que prácticamente coincidirá con la que se tendría al observar el objeto en verdadera magnitud en la realidad, de forma directa.

Vamos a ver un poco las Perspectivas y los tipos que hay:

4 – Perspectivas.

Las Perspectivas ocupan un lugar destacado dentro del ámbito de los Sistemas de Representación ya que expone de manera más concreta una ampliación de los fundamentos de las Proyecciones Diédricas y Triédricas Ortogonales.

Conviene diferenciar, no obstante, a fin de conseguir una mayor claridad, la variedad de Sistemas que existen. Para ello, se seguirá la clasificación reflejada en esta tabla:

PROYECCIONES	DIÉDRICA ORTOGONAL
	PERSPECTIVA COVENCIONAL O LIBRE		CABALLERA
			AXONOMÉTRICA	ISOMÉTRICA
				DIMÉTRICA
				TRIMÉTRICA
	PERSPECTIVA CÓNICA	ISOMÉTRICA
		DIMÉTRICA
		TRIMÉTRICA

Existen tres grandes grupos de Proyecciones. A continuación, vamos a exponer en que consiste cada una de ellas. Así, posteriormente, podremos pasar a explicar de una manera más concreta los importantes tipos de Perspectivas.

- Proyecciones Diédricas Ortogonales: Son las Proyecciones de diversas Vistas de un objeto, realizadas sobre Planos perpendiculares entre sí.

- Perspectiva convencional o libre: Consiste en la Representación de Objetos o cuerpos solidos, observados por el espectador desde un punto de vista fijo. Ofrece como resultado un dibujo convencional.

- Perspectiva Cónica: Es la que ofrece una Representación exacta, lo más parecida posible a la visión real, de los modelos que con ella se trazan.

Debido a su dificultad, y a la gran cantidad de conocimientos sobre geometría del espacio que son necesarios para realizar una perspectiva cónica, se creó un Sistema más sencillo: La Perspectiva Caballera, principalmente para los dibujos de maquinaria, carpintería y detalles constructivos. La Perspectiva convencional o libre dio la solución práctica adecuada, aunque su visión no fuese precisamente exacta.

Vamos a verla mas ampliamente:

Perspectiva Caballera.

De entre las variantes expuestas en el cuadro de la Tabla anteriormente vista, la Perspectiva Caballera es el tipo de Perspectiva más sencilla. Ésta Perspectiva elemental y rápida consiste en crear o situar los Planos y ejes de tal manera que sean paralelos a las tres direcciones del espacio: anchura, longitud y profundidad.

Ésta Perspectiva nos permite apreciar, a primer golpe de vista, la forma, los contornos y cualquier otro detalle que nos interese en la figura o del cuerpo representado.

Asimismo, y lo más importante, con ella se puede medir directamente sobre la figura.

El Sistema de Ejes Coordenados Ortogonales es el formado por tres Rectas que marcan tres direcciones: X, Y y Z.

Desde las tres direcciones serán perpendiculares entre sí: el ancho y el alto. La profundidad será oblicua a las otras dos. Para comenzar a dibujar, se han de situar previamente los tres ejes X, Y y Z, de forma que X y Z sean perpendiculares, e Y forme con éstos un ángulo cualquiera ( este será, por consiguiente, el eje oblicuo ). Para mayor simplicidad, se recomienda que los ángulos YX e YZ sean de 135º, es decir que comiencen su prolongación por el vértice de la bisectriz del Ángulo XZ.

Éstos tres Ejes determinan tres Planos, el XY, XZ y ZY, que forman entre ellos un triedro trirrectángulo. Como el Eje Y es el único oblicuo, tendrá que sufrir una reducción de medida respecto a los otros para que su efecto visual final se aproxime al máximo a la realidad.

Esta reducción con respecto a la unidad aplicable a XZ, puede ser cualquiera, pero las más usuales y de mejor efecto son las reducciones de 0,5 ; 0,6 y 0,8.

Si se Proyecta un Punto A cualquiera del espacio perpendicularmente sobre cada uno de los Planos de Coordenadas, tendremos las Proyecciones A1, A2 y A3. Cada una de estas Rectas AA2 y AA3 forman un Plano que corta el Eje Z en un Punto P. De la misma manera se pueden obtener los Puntos M y N sobre los Ejes X e Y. Si se observa con atención, se podrá ver que se ha formado un paralelepípedo rectangular en el que tres de sus aristas coinciden con los Ejes de Coordenadas. Este paralelepípedo tiene a A como vértice opuesto al Punto O, que es el origen de coordenadas.

Las longitudes OM=x ; ON=y ; OP=z, se llaman coordenadas del Punto A; son las que determinan la posición del Punto en el Espacio y las que corresponden a la anchura, longitud y profundidad, como ya se ha indicado anteriormente.

Fijémonos en estas dos Representaciones:

Representación 1

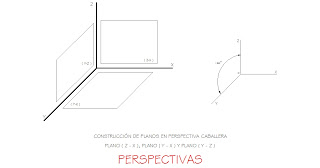
Representación 2

Representación 3

Una vez trazados los Ejes XYZ y determinado la reducción de Y, pasar a construir la escala: los Ejes X y Z tendrán unas unidades que, en el caso del Eje Y, se disminuirán aplicando el factor de reducción de 0,8. A continuación se trazará un cuadrado en el Plano XZ y en los Planos XY e YZ otros que, al ser vistos oblicuamente, presentarán las formas de dos romboides ( las cuatro paralelas al Eje Y están afectadas por la reducción 0,8 ).

Si nos fijamos en la Representación 3, vemos que se plantea uno de los problemas más importantes de la Perspectiva: el trazado de curvas o circunferencias en los Planos oblicuos.

Como podemos observar, en el Plano ZX la circunferencia está trazada con compás. Esto es así porque el aspecto que ofrece al espectador no está deformado, la circunferencia es paralela a él. En cambio, en los Planos XY e YZ, la circunferencia ya no ofrece el mismo aspecto, a causa de que toda la circunferencia oblicua al espectador queda convertida en una elipse, por las leyes geométricas.

Si observamos la manera de inscribir la circunferencia del Plano ZX en el cuadrado, trazando en éste las medianas y diagonales, se apreciará como estas Rectas tienen Puntos comunes con la circunferencia dada en: a, b, c, d, e, f, g, h. S i como en el caso de la Representación 1 y 2, se trazan en los Planos XY e YZ dos cuadrados iguales al que circunscribe a la circunferencia ( Representación 3 ), se verá como será sencillo obtener en ellos los ocho Puntos citados, realizando en su interior las diagonales y las medianas. Para hallar los Puntos a, c 9 y e de las diagonales, se utilizarán unas paralelas a los Ejes Y y Z desde los Puntos en los que las paralelas del Plano XZ ( que pasan por los citados Puntos comunes de la circunferencia y diagonales ) cortan a los Ejes X y Z.

El trazado de las circunferencias oblicuas o elipses habrá de realizarse a mano, y su puesta en limpio mediante plantillas trazadas al efecto.

Perspectiva Axonométrica.

La Perspectiva Axonométrica se diferencia esencialmente de la Perspectiva Caballera por el hecho de que entre los tres Ejes de Coordenadas XYZ no existe perpendicular alguna.

Como en la Caballera, los tres Ejes se unen en el vértice 0, pero formando ahora entre sí ángulos agudos y obtusos ( sus ángulos no pueden ser nunca Rectos, ya que éstos son privilegio de la Caballera ).

El único Eje que no cambia su posición es el Z, que sigue siendo vertical. Como los ángulos que forman entre sí no son Rectos, los tres Ejes han de sufrir una Reducción con respecto a la medida natural. Cuando la Reducción es igual en los tres Ejes ( o sea, cuando los ángulos que forman entre sí son iguales se llama Perspectiva Isométrica. Cuando sólo dos ángulos son iguales se llama Perspectiva Simétrica. Y cuando los tres ángulos son diferentes tendremos la Perspectiva Trimétrica.

La Reducción dependerá del valor de los ángulos que los Ejes formen entre sí.

Con todo esto que hemos determinado podemos deducir que:

1- Los tres Ejes XYZ, situados en el espacio real, son perpendiculares entre sí.

2- En la Perspectiva Axonométrica los Ejes forman ángulos obtusos ( mayores de 90º ).

3- Cada dos Ejes determinan un Plano, formando entre los tres un Triedro trirrectángulo.

4- Los tres Ejes y con ello los tres Planos, determinan las tres direcciones del Espacio real. Anchura, profundidad y altura.

El mecanismo de trazado es exactamente el mismo que el de la Perspectiva Caballera; lo único que se debe de tener presente es que las Rectas utilizadas han de ser paralelas a los Ejes XYZ que se han adoptado para realizar el dibujo.

Para una mayor facilidad en el trazado de la Perspectiva Axonométrica, se puede observar la siguiente Tabla de relación: en ella se encontrará la correspondencia entre los distintos valores angulares y de Reducción de los tres Sistemas: Isométrico, Simétrico y Trimétrico.

La Tabla queda reducida a unos pocos ejemplos de cada Sistema.

De los tres tipos de Perspectiva Axonométrica ( Isométrica, Dimétrica y Trimétrica ) la que destaca por su simplicidad y sencillez es la que vamos a ve ISOMÉTRICA.

La Perspectiva Axonométrica Isométrica es de los tres Sistemas Axonométricos la mas simple y rápida de realización. Con el fin de disponer de un procedimiento que proporcione unas mejores vistas que la Caballera, es interesante finalizar con unos comentarios breves sobre la Perspectiva Axonométrica Isométrica.

En la Tabla que hemos determinado anteriormente podemos ver que en la relación entre los valores angulares y de reducción de la Perspectiva Axonométrica Isométrica los tres ángulos del triedro forman entre sí ángulos iguales de 120º de abertura; es decir que la circunferencia se divide en tres partes.

De la misma manera que el coeficiente de reducción establecido por esta razón angular es de 81.6 mm para los tres Ejes.

Con ello se puede comprobar que se resuelven en una sola escala todas las medidas de los tres Ejes y que, por tanto, se simplifica el proceso de dibujo.

La gran ventaja que ofrece la Perspectiva Isométrica para el Trazado es la inclinación que los Ejes X e Y tienen con respecto a la horizontal: 30º.

En este Dibujo podemos observar que, utilizando el cartabón de modo que descanse por su cateto mayor sobre una regla, y teniendo en cuenta que ésta regla se deslice por el lateral del tablero sin perder su horizontalidad, se puede Trazar ya paralelas a los Ejes citados con gran rapidez, y sin dificultades.

Para dibujar correctamente cualquier superficie en Perspectiva Isométrica debe inscribirse la figura en un rectángulo o en un cuadrado y, proyectando isométricamente cualquiera de ellos, inscribir la figura u objeto que deseamos proyectar. ( lo vemos en el siguiente dibujo ).

Así como en la Perspectiva Caballera existe la posibilidad de Trazar las curvas de una circunferencia, con su verdadero aspecto, cuando están situadas en el Plano de frente XZ, en el Sistema Isométrico esto ya no es posible porque los tres Planos son oblicuos al espectador.

Por tanto en la Perspectiva Isométrica habrán de utilizarse procedimientos que faciliten este Trazado. Podría emplearse el mismo Sistema utilizando en la Caballera, pero con el fin de aplicar otras fórmulas que den nuevas posibilidades, se utilizará como figura sustitutiva de la elipse al óvalo, es decir, la visión que ofrece la circunferencia cuando se encuentra en un Plano oblicuo.

Como podemos observar en este dibujo el procedimiento para Trazar estos Óvalos es el mismo que el utilizado para el Trazado de Polígonos.

Por último, y ya mirando desde un punto de vista profesional de la edificación, vamos a determinar el último tipo de Perspectiva que es la que más se acerca a la realidad en la vista en 3 dimensiones de un objeto. Que es la Perspectiva Cónica, aunque también debemos de decir que es la más complicada y para desarrollarla hace falta tener un buen conocimiento de las técnicas del espacio.

Es utilizada en todos los ámbitos Técnico Profesionales. Delineación, Arquitectura e Ingeniería pero es en la Arquitectura donde su utilización se hace especialmente importante como veremos:

Vamos a determinar los aspectos más importantes de la misma:

Perspectiva Cónica.

Como modelo volumétrico que acerca el objeto a su representación más próxima a lo real, contribuye a complementar la documentación gráfica dentro de un Proyecto. A la síntesis del objeto que representan los Planos de Planta y Alzado, se contrapone la Perspectiva Cónica, con una imagen del objeto como se puede ver en la realidad.

Lógicamente que es este el tipo de Perspectiva que los Arquitectos o Delineantes utilizan para sus proyectos, para la representación del volumen final de una construcción. Así se verá el resultado final del Proyecto desarrollado en su totalidad. Eso sí, comentar que la Perspectiva Cónica no es un documento obligatorio en el Proyecto, pero es de gran ayuda para el resultado final del mismo.

Bien, pues para poder Representar o Interpretar objetos y volúmenes en un Plano, son necesarias una serie de Vistas que nos describan el objeto de una manera completa ofreciéndonos la máxima información posible sobre él. Estas Vistas, hechas desde todas las posiciones necesarias, nos delimitan y definirán el objeto, ayudándonos a su compresión. Según sea el objeto, se necesitarán más o menos Vistas para Representarlo.

Como se puede comprobar, para representar una esfera, será suficiente con una sola Vista. Sin embargo, para Representar un objeto más complicado como lo es un edificio serán necesarias varias.

Por ello la Perspectiva Cónica es la que se utiliza finalmente para la Representación de un Edificio.

Se entiende por Perspectiva Cónica aquella que Representa al objeto tal y como puede ser observado desde un punto de vista real. Como hemos determinado anteriormente su aplicación más inmediata es la Arquitectura, el interiorismo, etc..

La Perspectiva Cónica propone la Visión más real posible del objeto o del espacio antes de ser construido.

En este Sistema de Representación, el espectador se sitúa próximo al objeto, por lo que las Rectas Proyectantes dejan de ser paralelas entre sí, para pasar a formar parte de un Sistema de haces Cónicos, convergentes en un Punto al que se llama Foco.

Estos haces convergentes se ven interceptados por un Plano perpendicular, situado entre el objeto y el observador, al que se llama Plano del cuadro. La intersección de las visuales con dicho Plano del cuadro determinará la Proyección Cónica del objeto.

Si observamos el dibujo siguiente el observador se encuentra situado sobre un Plano Horizontal, llamado Plano Geometral, que es perpendicular al Plano del cuadro; la línea de intersección de ambos ( LT ), se llama línea de tierra. El Punto desde el que se observan el cuadro y el objeto es el Punto de vista V. La Línea Horizontal H, situada en el Plano del cuadro y paralela a la línea de tierra, se llama línea de horizonte; corresponde a la intersección de un imaginario Plano Horizontal, perpendicular al Plano del cuadro, ya la misma altura sobre la horizontal que el Punto de vista del observador.

Las características esenciales de la Perspectiva Cónica son:

a) Es la Representación más parecida a una visión real del objeto, desde un Punto de vista determinado.

b) No se puede medir directamente sobre ella, como en la Perspectiva Caballera.

c) Las Líneas pierden su paralelismo y visualmente, se juntan en el horizonte.

Los elementos principales de una Perspectiva Cónica, los cuales los observamos en el dibujo anterior son los siguientes:

1) El Objeto. Los cuerpos lineales y ortogonales son los más sencillos de representar.

2) El Punto de Vista ( PV ). Es el Punto desde el que se observa el Objeto. Su colocación es decisiva para la expresión de la Perspectiva; se determina mediante la correcta elección de su distancia al Plano del cuadro, su altura respecto de la horizontal y la abertura de visión.

3) El Cono de Rayos Visuales. Genera la Representación, sobre el Plano, del cuadro de los Puntos de Intersección de los rayos con el objeto; los valores recomendables de los ángulos visuales corresponden a 30 – 45º.

4) Rayo Principal. Es la visual perpendicular al Plano del Cuadro; es la distancia más corta desde el observador hasta el objeto y representaría la altura del cono de rayos visuales. La distancia del rayo principal debe ser como mínimo una vez y media la mayor longitud del objeto a representar.

5) Plano del Cuadro. Es el Plano sobre el que se proyecta el objeto; se le supone transparente y, preferiblemente vertical y perpendicular al cono de rayos visuales. El alejamiento del Plano del Cuadro, respecto del Punto de Vista, determinará el tamaño de la imagen.

6) Plano Geometral. Es el Plano Horizontal que sustituye al suelo y sobre el que se sitúan el observador y el Plano del Cuadro.

7) Plano Objetivo. Es la prolongación del Plano Geometral por detrás del Plano del Cuadro; sobre él descansa el objeto que se quiere representar.

8) Línea de Tierra. Es la Línea de intersección que forman el Plano Geometral y el Plano del Cuadro.

9) Plano de Horizonte. Es el Plano paralelo al Plano Geometral que contiene al Punto de Vista.

10) Línea de Horizonte. Es la Línea que forma la intersección del Plano de Horizonte con el Plano del Cuadro; es una Línea paralela a la Línea de Tierra.

A la Perspectiva Cónica podemos darle una clasificación. La Perspectiva Cónica es paralela a su forma de realización. Básicamente es ésta:

A) Perspectiva Central. Un solo Punto de Fuga. Las Líneas de profundidad convergen en un Punto, llamado Punto de Fuga.

B) Perspectiva Oblicua. Dos Puntos de Fuga. Las Líneas de profundidad y anchura convergen en dos Puntos, llamados Puntos de Fuga.

C) Perspectiva de Cuadro Inclinado. Dos o tres Puntos de Fuga. Las Líneas de Profundidad, anchura y altura convergen en tres Puntos de Fuga.

Con esto hemos terminado la exposición de los llamados Sistemas de Representación, desde los Sistemas utilizados en dibujo técnico ( Geometría Descriptiva ) los Sistemas Diédrico y Triédrico, hasta el Sistema más utilizado en 3 dimensiones y para la Representación de dibujos Arquitectónicos y de Delineación las Perspectivas.

Todo ello para una mejor visión del espacio tanto en 2 como en 3 dimensiones que es la realidad pura.

Por último vamos a determinar algunos Ejemplos de PERSPECTIVAS, para que se vea el poder de este Sistema de Representación con respecto a la realidad:

1 )

2 )

3 )

4 )